Today we will discuss about a data-structure, segment tree which again deals with Range Query and Update as Binary Indexed Tree.
Range Minimum Query(RMQ) is a classic computer science problem, which asks for minimum value, repeatedly in the given ranges. Let us assume an array { 2, 4, 6, 7, 5, 3, 1, 8 }. And we would be getting queries like, minimum in the range 4 - 5, 0 - 3, etc. Here the minimum operation can be anything like maximum, sum, etc.
One easier way to solve this problem(RMQ) is to pre-process information. In case of minimum, pre-processed info can be an array such that value at an index corresponds to minimum value encountered until that index in input array.
ProcessedArray[i] = min{ inputArray[0], inputArray[1] ... inputArray[i] }. Better dynamic programming approach would do pre-processing in O(n). But the problem is updating a value in inputArray would make processed array, completely invalid in the worst case. So, updates would be very costly.
Naive approach is to check all the elements in the range for minimum value and complexity in this case would be O(n) in the worst case, which is un-affordable in case of huge number of queries.
Segment trees would be a better candidate for this problem as it stores minimum values of intermediate ranges in tree nodes and original values in tree leaf nodes. This may lead to a space complexity of twice the number of elements in the original input approximately. But complexity of query reduces to log N which is promising. Segment tree is balanced and complete binary tree. It could be considered as a heap as it has characteristics of completeness and parent node's value is a function of child nodes, in RMQ it is minimum function. So, it could be stored in Array, as we do in Binary Heap.
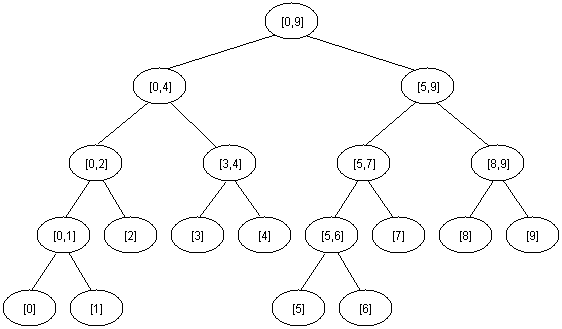
Each node stores the minimum value of the given range. Range is depicted inside the circle. For instance [0, 9] means, it stores the minimum value of the range 0 - 9. Now query for a range could easily be done in log N times. Let us say, if we need to Query the range 0 - 6, it could be divided into 0 - 4 and 5 - 6, which could be got from tree nodes easily. I am adding up source code written in C++ for the same below. Questions are welcome.
Code below, is for Demo Purpose, not of production quality.
Thanks for Reading.
double Log2(double in)
{
return log(in)/ log(double(2));
}
int NearestPowerOfTwo(int in)
{
return pow(2, ceil(Log2(in)));
}
class SegmentTree
{
public:
SegmentTree()
{
treeArray = NULL;
}
~SegmentTree()
{
delete [] treeArray; treeArray = NULL;
}
void CreateTree(int *inArray, int length);
void InitializeTree(int internalIndex, int *inArray, int start, int end);
int QueryTree(int internalIndex, int start, int end, int rangeStart, int rangeEnd)
{
// Pre-condition check.
if( rangeStart > end || rangeEnd < start)
return -1;
// Check the present range overlap
if( start >= rangeStart && end <= rangeEnd)
return treeArray[internalIndex];
int left = QueryTree(2 * internalIndex + 1, start, (start + end) / 2, rangeStart, rangeEnd);
int right = QueryTree(2 * internalIndex + 2, (start + end) / 2 + 1, end, rangeStart, rangeEnd);
if( left == -1)
return right;
else if( right == -1)
return left;
else
return (left < right) ? left : right;
}
void UpdateTree(int index, int value);
private:
int *treeArray;
int treeLength;
};
void SegmentTree::CreateTree(int *inArray, int length)
{
// Create Tree here...
treeLength = 2 * NearestPowerOfTwo(length) - 1;
treeArray = new int(treeLength);
InitializeTree(0, inArray, 0, length - 1);
}
void SegmentTree::InitializeTree(int internalIndex, int *inArray, int start, int end)
{
// Base condition.
if( start >= end)
{
treeArray[internalIndex] = inArray[start];
return;
}
InitializeTree(internalIndex * 2 + 1, inArray, start, (start + end) / 2);
InitializeTree(internalIndex * 2 + 2, inArray, (start + end) / 2 + 1, end);
if( treeArray[internalIndex * 2 + 1] < treeArray[internalIndex * 2 + 2])
treeArray[internalIndex] = treeArray[internalIndex * 2 + 1];
else
treeArray[internalIndex] = treeArray[internalIndex * 2 + 2];
}
void SegmentTree::UpdateTree(int index, int value)
{
int indexToModify = treeLength / 2 + index;
treeArray[indexToModify] = value;
int indexToCorrect = (indexToModify - 1) / 2;
while(indexToCorrect >= 0)
{
if( treeArray[indexToCorrect * 2 + 1] < treeArray[indexToCorrect * 2 + 2])
treeArray[indexToCorrect] = treeArray[indexToCorrect * 2 + 1];
else
treeArray[indexToCorrect] = treeArray[indexToCorrect * 2 + 2];
if( indexToCorrect == 0) break;
indexToCorrect = (indexToCorrect - 1) / 2;
}
}
